Nekromanti Ett geometriproblem

[Wilmer]

Jag har ett matteproblem jag skulle upp uppskatta hjälp med. Fyra kvartscirklar är i en kvadrat (sidan 1). Jag ska räkna ut arean av C.

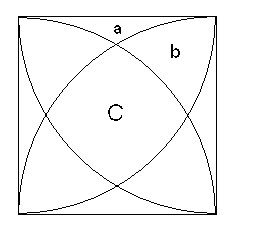
För att lösa det lätt och snyggt gjorde jag ett ekvationssystem.

c+3b+2a = Pi/4
b+2a = 1 - Pi/4
c+2b = Pi/2 - 1

Men eftersom det mellersta egentligen är den övre minus den undre hjälper det ju föga, skiten går runt hela tiden! Hjälp.

 

[Dimfrost]

Jag skulle lösa det genom att hitta ekvationer för linjerna (eftersom de är cirklar är det inte så svårt), dela upp C i två lika stora delar genom en vertikal linje genom mitten och sedan integrera.


/Dimfrost

 

[Man Mountainman]

Okej, här kommer en lösning som är lite mer renodlat geometrisk än Dimfrosts analysvariant. Lösningen är mestadels due to Feliath, men jag hjälpte till litegrann. ^_^

Först konstaterar vi att de röda linjerna i bilden nedan alla är cirkelradier, och alltså bildar en likbent triangel. Därmed är den gröna vinkeln i bilden 30°. Vi kallar den alfa.

Alfa bildar en cirkelsektor, som synes i bilden nedan.

Det finns formler för att beräkna längden på kordan C och den blå arean, som vi kallar A. Dessa formler är:

respektive

Now, om vi går in närmare så ser vi att C bildar en rätvinklig triangel tillsammans med kanten på kvadraten (den röda triangeln i bilden nedan).

Triangeln har, som vi tydligt kan se, arean A + a/2. Men triangelns area är känd för oss, eftersom vi har värdet på såväl C (hypotenusan) som dess längsta katet (som ju är halva vår kvadrat, det vill säga 1/2). Vi kan alltså beräkna triangelns area med Pytagoras sats:

Nu kan vi lösa ut a:

Och vips, så har du bara två okända i ditt ekvationssystem istället för tre, och kan lösa uppgiften!

/Kalle

 

[Krille]

Lite mer kul saker: vet vi den blå ytan och sträckan c så kan vi räkna ut arean C direkt.

Se, din trevliga triangel visar att om den gröna vinkeln alfa är 30 grader, så måste det även vara 30 grader från andra hållet också. Det gör att vinkeln mellan mittencirkelsektorerna också är 30 grader.

Det är för fan bara att tacka och ta emot, för om den blå ytan och sträckan c är kända så är dessa lika stora även i mittencirkelsektorerna. Och då är arean C lika med c i kvadrat plus fyra blå areor.

 

[Man Mountainman]

Right on!

Det stämmer ju fint, det. Så vackert att se folk arbeta vidare på varandras lösningar för att nå än högre enkelhet och elegans. Jag får nästan en tår i ögat.

/Kalle