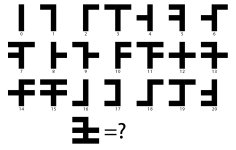You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Räkneklurigheter
- Thread starter Caligo
- Start date
Rangertheman
Myrmidon
- Joined
- 15 Dec 2015
- Messages
- 4,481
23?
Nix
Hägerstrand
För sexig för att vara bybo
- Joined
- 2 Dec 2022
- Messages
- 3,221
Det ser väl ut som att det borde vara 61? Räknesystemet bygger på bas 4, men det känns mer chifferartat än som ett riktigt räknesystem när det slutar vid 4^3 (alltså 1000 i det här systemet) eftersom man inte kan förlänga mittstolpen hur mycket man vill utan att det blir oklart hur många 0:or man passerar.Ok... Jag jobbar vidare med mitt språk och dess skrivtecken. Nedan är tecken som motsvarar tal 0-20. Vilket tal är sista tecknet (med frågetecknet)?
View attachment 24834
Det är ju egentligen bara tre siffertecken i systemet.
edit: försökte låta mer pedagogisk.
Last edited:
Rymdhamster
ɹǝʇsɯɐɥpɯʎɹ
3 uppochner = 12
+ 13
Alltså 25
Eller
15 upp och ner = 60
+1
Alltså 61
Inget av svaren kändes uppenbart, och jag tror det går att hitta på fler alternativ beroende på hur dina räkneregler (Som jag inte vet något om) fungerar.
+ 13
Alltså 25
Eller
15 upp och ner = 60
+1
Alltså 61
Inget av svaren kändes uppenbart, och jag tror det går att hitta på fler alternativ beroende på hur dina räkneregler (Som jag inte vet något om) fungerar.
Det ser väl ut som att det borde vara 61? Räknesystemet bygger på bas 4, men det känns mer chifferartat än som ett riktigt räknesystem när det slutar vid 4^3 (alltså 1000 i det här systemet) eftersom man inte kan förlänga mittstolpen hur mycket man vill utan att det blir oklart hur många 0:or man passerar.
Det är ju egentligen bara tre siffertecken i systemet.
edit: försökte låta mer pedagogisk.
61 borde det vara ja. Med vad vi har sett så kan man bara skriva talen 0-63. (Förutom mitt-stapeln så är det sex stycken streck (tre till vänster och tre till höger) som antingen kan vara där eller inte vara där. Således 2^6 möjliga kombinationer)
Vilket ju blir samma sak som 4^3, men är sant oavsett tänkt bas.
Hägerstrand
För sexig för att vara bybo
- Joined
- 2 Dec 2022
- Messages
- 3,221
mnja (eller ja det är sant att 2^6 ger samma resultat, men det är ett ointuitivt sätt att se på det om man vill förstå systemet). Siffrorna är 1-3, på översta raden. Därefter kommer siffran 1 på rad två som då är tiotalsraden, och alltså 10 i bas-4 eller 4 i bas-10.61 borde det vara ja. Med vad vi har sett så kan man bara skriva talen 0-63. (Förutom mitt-stapeln så är det sex stycken streck (tre till vänster och tre till höger) som antingen kan vara där eller inte vara där. Således 2^6 möjliga kombinationer)
Vilket ju blir samma sak som 4^3, men är sant oavsett tänkt bas.
Sen 11, 12, 13, 20 (dvs symbolen för 2 på mittenraden, symbolen för 0 på översta raden, 8 i bas-10) etc. När ettan dyker upp på tredje raden är det då 4^2, eller 100 i bas-4.
Att se på systemet som symboler för 0-63 är att se på det som ett chiffer. Om man ska se det som ett räknesystem så är det ett räknesystem för ett samhälle där entalen slutar vid 3 (vilket är exakt lika rimligt som att tänka att de slutar vid 9) och då vill man kunna räkna till godtycklig storlek på talen.
Det jag menar är problemet är att 16, 64 och 256 blir svåra att särskilja från varandra. Jag tänkte först att det också skulle vara ett problem om 64 representeras av symbolen för 1 och symbolen för 0, men det är egentligen inte så konstigt. Det blir ungefär på samma sätt som vi räknar tusental.
Last edited:
Rymdhamster
ɹǝʇsɯɐɥpɯʎɹ
14 upp och ner + 1 upp och ner +1 = 61 är också ett alternativ.
16 bak och fram + 17 + 12 = 61
Jag börjar luta åt att 61 är rätt svar och 25 antingen är en avvikelse i ditt system, eller bryter mot någon regel som gör att det diskvalificeras.
16 bak och fram + 17 + 12 = 61
Jag börjar luta åt att 61 är rätt svar och 25 antingen är en avvikelse i ditt system, eller bryter mot någon regel som gör att det diskvalificeras.
mnja (eller ja det är sant att 2^6 ger samma resultat, men det är ett ointuitivt sätt att se på det om man vill förstå systemet). Siffrorna är 1-3, på översta raden. Därefter kommer siffran 1 på rad två som då är tiotalsraden, och alltså 10 i bas-4 eller 4 i bas-10.
Sen 11, 12, 13, 20 (dvs symbolen för 2 på mittenraden, symbolen för 0 på översta raden, 8 i bas-10) etc. När ettan dyker upp på tredje raden är det då 4^2, eller 100 i bas-4.
Att se på systemet som symboler för 0-63 är att se på det som ett chiffer. Om man ska se det som ett räknesystem så är det ett räknesystem för ett samhälle där entalen slutar vid 3 (vilket är exakt lika rimligt som att tänka att de slutar vid 9) och då vill man kunna räkna till godtycklig storlek på talen.
Det har absolut ingenting med chiffer att göra. Att det finns 2^6 olika symboler i systemet är bara en enkel observation baserad på hur symbolerna kan skapas, och har inte så mycket att göra med hur de skall tolkas.
Jag skulle snarare säga att det är bas 64, där varje symbol är en "siffra". Vore det bas 4 så borde det bara finnas 4 olika "siffror" som sedan kombineras till olika tal.
Nu är det 64 olika "siffror", även om sättet de konstrueras på är baserat på de 4 olika varianter man kan göra av två horisontella streck.
Hägerstrand
För sexig för att vara bybo
- Joined
- 2 Dec 2022
- Messages
- 3,221
Ja. Om du låter . representera 0-strecket så har duVore det bas 4 så borde det bara finnas 4 olika "siffror" som sedan kombineras till olika tal.
. = 0
_. = 1
._ = 2
_._ =3
Det är deras tre siffror.
Sen har du ental på översta raden, tiotal på mellersta och hundratal på nedersta. Om det här är talsystemet i ett hittepå-världsbygge (vilket jag tolkar tråden som) så är det ett samhälle där man räknar i bas-4.
Att tänka på det som 64 olika symboler och att det därför är ett bas 64-system är alltså ett chiffer-perspektiv snarare än ett världsbygge-perspektiv. Symbolen för 22 (i bas 10) bör utläsas med ord för ett-hundra-ett-tio-två (eventuellt med avvikelser precis som svenskan eller franskan, men fortfarande med samma system), och inte med ett av 63 olika ord för ental.
Last edited:
Hägerstrand
För sexig för att vara bybo
- Joined
- 2 Dec 2022
- Messages
- 3,221
JohanL
Champion
- Joined
- 23 Jan 2021
- Messages
- 10,149
Jag ser hur det fungerar (varje horisontellt streck har ett exponentiellt ökande värde, så att det är ett binärt tal representerat grafiskt) men orkar inte räkna ut det.
Det blir sjukt opraktiskt att använda och konstruktören borde ha stryk.
(Det är också tvivelaktigt eftersom det inte går att räkna särskilt högt med det.)
Det blir sjukt opraktiskt att använda och konstruktören borde ha stryk.
(Det är också tvivelaktigt eftersom det inte går att räkna särskilt högt med det.)
Rickard
Urverk speldesign
Jag trodde det också till en början, men när jag läste vad andra skrev insåg jag att det var bara toppen som "snurrade". De andra strecken bara höll räkningen på antalet varv.Jag ser hur det fungerar (varje horisontellt streck har ett exponentiellt ökande värde
JohanL
Champion
- Joined
- 23 Jan 2021
- Messages
- 10,149
Samma sak, väl? Topp vänster är 0 eller 1, topp höger är 0 eller 2, mitten vänster är 0 eller 4, mitten höger är 0 eller 8, och så vidare. Binärt tal representerat med geometri.Jag trodde det också till en början, men när jag läste vad andra skrev insåg jag att det var bara toppen som "snurrade". De andra strecken bara höll räkningen på antalet varv.
Det snabba sättet att komma fram till 61 är att se att talen som kan representeras är 0 - 63, och det saknas 2 för att det strecket är borta.
Jag tar det som en komplimangDet blir sjukt opraktiskt att använda och konstruktören borde ha stryk.
Som andra skriver så är det ju ett binärt tal representerat grafiskt.
Topp vänster = 1
Topp höger = 2
Mitten vänster = 4
Mitten höger = 8
Botten vänster = 16
Botten höger = 32
Det är bara att plussa ihop sträcken
0b111101 = 61
Om man istället skulle lägga den på sidan skulle man ju kunna förlänga mittenstrecket och ha så många sträck man behöver (om man ens skriver från vänster/höger).
Topp vänster = 1
Topp höger = 2
Mitten vänster = 4
Mitten höger = 8
Botten vänster = 16
Botten höger = 32
Det är bara att plussa ihop sträcken
0b111101 = 61
Om man istället skulle lägga den på sidan skulle man ju kunna förlänga mittenstrecket och ha så många sträck man behöver (om man ens skriver från vänster/höger).
Rymdhamster
ɹǝʇsɯɐɥpɯʎɹ
Ah, nu fattar jag hur man ska tänka! Tack för förklaringen!Som andra skriver så är det ju ett binärt tal representerat grafiskt.
Topp vänster = 1
Topp höger = 2
Mitten vänster = 4
Mitten höger = 8
Botten vänster = 16
Botten höger = 32
Det är bara att plussa ihop sträcken
0b111101 = 61
Om man istället skulle lägga den på sidan skulle man ju kunna förlänga mittenstrecket och ha så många sträck man behöver (om man ens skriver från vänster/höger).
Om räknesystemet kommer från en kultur som rätt sällan har behov av större tal än 63 går det ju att lösa med ett sekundärt system som räknar hur många "högar" med 63 föremål man har. Typ ett antal prickar över/under siffran.
Lite som att räkna hur många gross eller hur många dussin man har.
Jag har tänkt att man bara lägger til en symbol och då får 6 bitar till mrn visst kan man lägga symbolen ner och lägga till bitar.Som andra skriver så är det ju ett binärt tal representerat grafiskt.
Topp vänster = 1
Topp höger = 2
Mitten vänster = 4
Mitten höger = 8
Botten vänster = 16
Botten höger = 32
Det är bara att plussa ihop sträcken
0b111101 = 61
Om man istället skulle lägga den på sidan skulle man ju kunna förlänga mittenstrecket och ha så många sträck man behöver (om man ens skriver från vänster/höger).